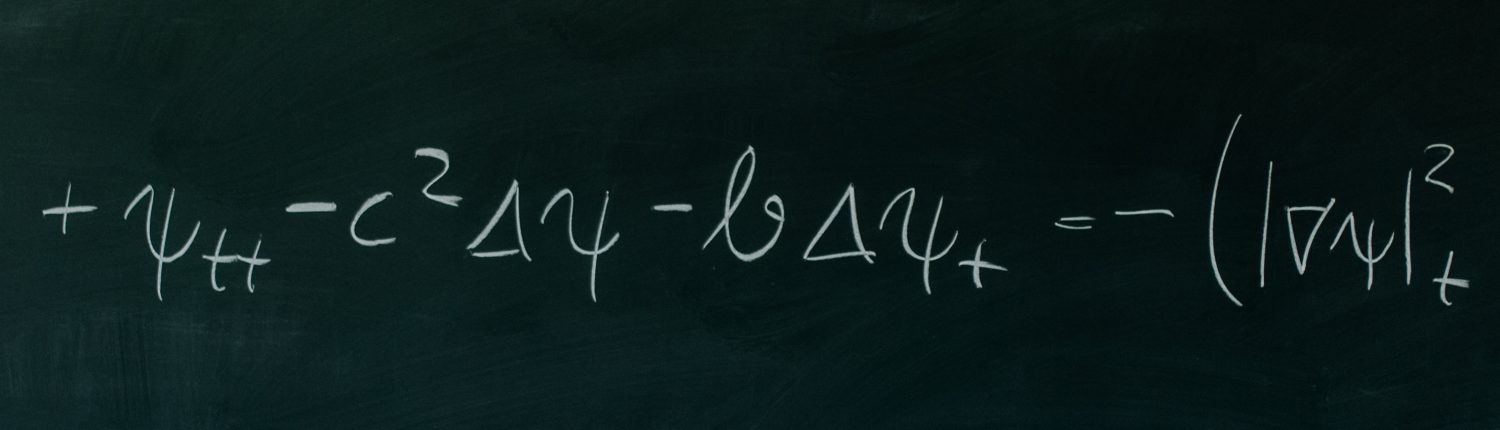Women of Mathematics: Barbara Kaltenbacher
Country: Austria
Affiliation: Universität Klagenfurt, Austria
Field of Research: inverse problems, regularization methods, parameter identification in partial differential equations, optimization with PDE constraints, direct and inverse problems in piezoelectricity and magnetics, nonlinear acoustics
1.) Why did you choose this formula?
Because it is a formula I am working with at the moment. It describes the nonlinear propagation of high-intensity focused ultrasound, as can be seen when it is used to disintegrate kidney stones, for example. This model is what is known as a partial differential equation, which involves various physical parameters. I am currently looking into how the solution of this equation changes as the tau parameter (relaxation time) approaches zero.
2.) What made you decide to study Mathematics?
I always enjoyed studying Mathematics at school – and I definitely have my high-school teacher to largely thank for that as she helped and encouraged us a great deal. I wasn’t your typical maths geek, though! I was interested in a lot of other things at school and I had to work really hard when I first started studying. It only really all clicked into place properly after the first few semesters.
3.) What do you like so much about Mathematics?
I like the fact that there are definitive answers in the sense that a mathematical statement can only be true or false and a mathematical proof is absolutely watertight and cannot be disputed (provided that it is correct in the first place, of course). On the other hand, it can be extremely hard work to get to that stage and proofs have been known to haunt my dreams at times.
You’ve also got the chance to work with people from all around the world – and they are basically always like-minded people who are just as fascinated by Mathematics. There are also plenty of exciting fields of application, meaning that there is more or less always chance to learn something new.
4.) How does Mathematics influence our lives on a daily basis?
There are so many applications within my own field of research alone, including all medical imaging processes, which simply couldn’t exist without advanced mathematical algorithms. In actual fact, Mathematics is at the heart of all modern technology, ranging from algorithms used to process signals in telecommunications to the control systems for industrial facilities. It is often the case that mathematical tools are based on results from pure basic research, for which no real-life applications were considered when they first came about. And, of course, the process of actually applying them often requires close collaboration with colleagues from the fields of Engineering, Medicine, Business and so on. But there’s still lots of work to be done on pure basic research within Mathematics too.
5.) Have you experienced a special Mathematics moment?
Special moments happen all the time when the basic idea behind a proof comes to me or once I have added the final little part of the puzzle to finish it off. There are special moments like this in teaching too, such as when I realise that the students are taking on board and truly understanding what I am trying to tell them about.
6.) What advice would you give future mathematicians to help them on their way?
At the end of the day, Mathematics is a gender-neutral science – both in terms of the content covered and the ways of working. That makes it all the more crazy that there are still fewer female mathematicians than male ones. It’s certainly a positive and natural development that this difference in numbers is decreasing with every generation. But we need to reach a balance much more quickly. There are still girls and young women who simply don’t have enough confidence in themselves when it comes to Mathematics – and that comes across first when they are choosing what to study and then later on when they need to assert their position within the academic world. We are still sadly seeing way too many talented candidates slip through the net as a result.